Discover and read the best of Twitter Threads about #統計
Most recents (24)
#統計 念の為のコメント
1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。
2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。
以上の誤りを信じている人達をよく見る。続く
1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。
2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。
以上の誤りを信じている人達をよく見る。続く
#統計
1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。
これについてはツイッター上で繰り返し非常に詳しく解説して来ました。
ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
1️⃣「t検定の使用が適切なためには、母集団が正規分布に従っていることが必要である」という考え方は誤り。
これについてはツイッター上で繰り返し非常に詳しく解説して来ました。
ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
#統計
2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。
これについてもツイッター上で繰り返し非常に詳しく解説して来ました。
ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
2️⃣「Wilcoxonの順位和検定=Mann-WhitneyのU検定であれば、無条件使用は適切である」という考え方も誤り。
これについてもツイッター上で繰り返し非常に詳しく解説して来ました。
ツイログ検索
↓
twilog.togetter.com/genkuroki/sear…
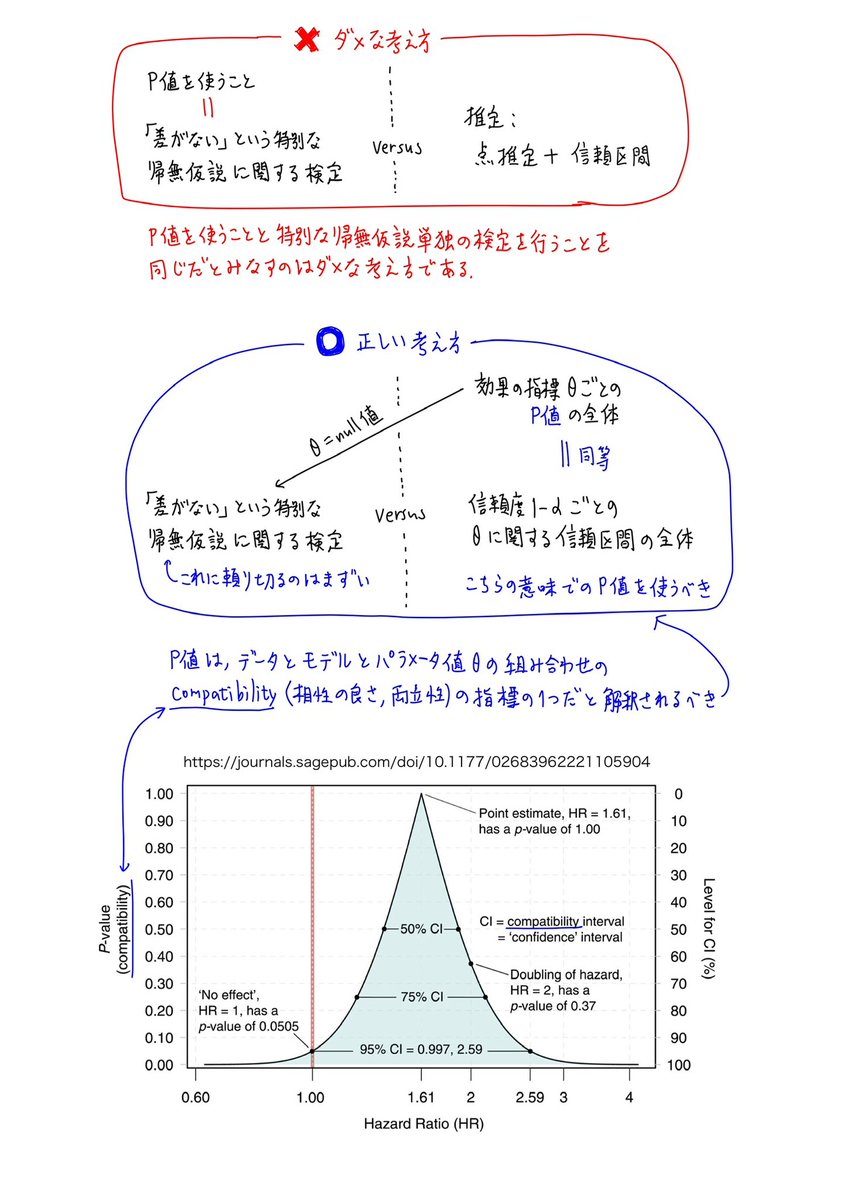
#統計 speakerdeck.com/taka88/pzhi-fa… のp.7からp.8への流れは、natureの記事の内容を誤解させるような、よろしくない解説の仕方だと思いました。
「差がない」という特別な帰無仮説の検定だけで勝負を決めようとすることへの批判をP値そのものへの批判とみなすことは、よく見る杜撰な考え方です。続く

「差がない」という特別な帰無仮説の検定だけで勝負を決めようとすることへの批判をP値そのものへの批判とみなすことは、よく見る杜撰な考え方です。続く


#統計 実際、natureの記事 nature.com/articles/d4158… ではcompati{ble,bility}が重要キーワードになっており、P値が
データ、モデル、パラメータ値のcompatibility(相性の良さ、両立性)の指標の1つ
とみなされることを詳しく説明しています。
この部分に触れずにこの記事を引用しても無意味。続く
データ、モデル、パラメータ値のcompatibility(相性の良さ、両立性)の指標の1つ
とみなされることを詳しく説明しています。
この部分に触れずにこの記事を引用しても無意味。続く

#統計 natureのその記事を読んでいるならば、P値のcompatibilityとしての解釈について知り、添付画像のように、ダメな考え方と正しい考え方を区別できるようになっているはずなのです。
否定するべき対象にP値そのものが含まれていないことに注目!
続く
否定するべき対象にP値そのものが含まれていないことに注目!
続く
このツイートの存在にずっと気付いてなくて、昨晩読んでしまって笑い転げた。
やっぱり「知的レベルが低い」としか言いようがない。
今時の中学生はこの手のことを言うと馬鹿にされることをネットで見てよく知っているので、現代的には中学生にも馬鹿にされるレベルだと思います。
やっぱり「知的レベルが低い」としか言いようがない。
今時の中学生はこの手のことを言うと馬鹿にされることをネットで見てよく知っているので、現代的には中学生にも馬鹿にされるレベルだと思います。
#統計
統計学ファンであれば、ゲルマンさんのブログで成田祐輔さんに関するNew York Timesでの記事が話題にされていることをすでに知っているはず。
ゲルマンさんのブログで悪い意味で取り上げられることは統計学方面では相当に怖いことだと思われます。
statmodeling.stat.columbia.edu/2023/02/13/yal…
統計学ファンであれば、ゲルマンさんのブログで成田祐輔さんに関するNew York Timesでの記事が話題にされていることをすでに知っているはず。
ゲルマンさんのブログで悪い意味で取り上げられることは統計学方面では相当に怖いことだと思われます。
statmodeling.stat.columbia.edu/2023/02/13/yal…
#統計 リンク先に飛ぶのが面倒な人は添付画像の最初の部分だけに目を通すだけで雰囲気が分かると思います。
最後まで取っておいた最高のネタは専門の中に確率統計が入っていること(笑)
ゲルマンさんによれば【馬鹿げた操作変数法のパロディのようなもの】らしい。
statmodeling.stat.columbia.edu/2023/02/13/yal…
最後まで取っておいた最高のネタは専門の中に確率統計が入っていること(笑)
ゲルマンさんによれば【馬鹿げた操作変数法のパロディのようなもの】らしい。
statmodeling.stat.columbia.edu/2023/02/13/yal…

#統計
正確な説明にこだわっているようなのであえてコメント。
線形回帰でこだわるべき条件は「残差が正規分布」よりも「残差が独立同分布」の方です。
残差が非正規分布のi.i.d.のときの線形回帰は、非正規母集団のt検定と同じようにうまく行ったり、行かなかったりします。詳しい解説に続く。
正確な説明にこだわっているようなのであえてコメント。
線形回帰でこだわるべき条件は「残差が正規分布」よりも「残差が独立同分布」の方です。
残差が非正規分布のi.i.d.のときの線形回帰は、非正規母集団のt検定と同じようにうまく行ったり、行かなかったりします。詳しい解説に続く。
#統計 例で説明します。
まず、残差がi.i.d.ではないが、残差全体は正規分布に従う場合があることの説明。
添付画像がそのような場合の例になっています。
データの散布図(青点達)を見ると、この場合には単純な線形回帰の適用が不適切であることは明らか。続き#
nbviewer.org/github/genkuro…
まず、残差がi.i.d.ではないが、残差全体は正規分布に従う場合があることの説明。
添付画像がそのような場合の例になっています。
データの散布図(青点達)を見ると、この場合には単純な線形回帰の適用が不適切であることは明らか。続き#
nbviewer.org/github/genkuro…

#統計 この例は回帰直線を2本にする必要があります。
1本の回帰直線に関する残差の値全体の分布は正規分布になります。
添付画像①から残差の分布がxへの依存性が分かる。
添付画像②はxを無視すると残差全体は正規分布になることの確認。(理論的にそうなることも確認済み)
続く

1本の回帰直線に関する残差の値全体の分布は正規分布になります。
添付画像①から残差の分布がxへの依存性が分かる。
添付画像②はxを無視すると残差全体は正規分布になることの確認。(理論的にそうなることも確認済み)
続く


#統計 P値や信頼区間に関する大学での講義は(数え切れないくらい強調していることですが)、論文 journals.sagepub.com/doi/10.1177/02… の内容(過信や自信過剰を引き起こさない考え方)に従うように改訂されるべきだと思います。
過去の大学の講義のほとんどがその意味では失格。
過去の大学の講義のほとんどがその意味では失格。
#統計 帰無仮説は統計モデルのパラメータの値に関する仮説になっており、P値を得るための確率の(近似)計算は帰無仮説下の統計モデル内で行うことになるので、統計モデルについての説明がない仮説検定の説明は最初から相手にする価値がないということになります。
#統計 仮説検定における「統計モデル」は「P値の計算に使われる数学的仮定の全体」のようにざくっと定義しておくと便利です。
例えば、P値の計算に確率の近似計算を使うならば、その近似がうまく行くという条件が統計モデルの中に含まれていると考えると便利。
例えば、P値の計算に確率の近似計算を使うならば、その近似がうまく行くという条件が統計モデルの中に含まれていると考えると便利。
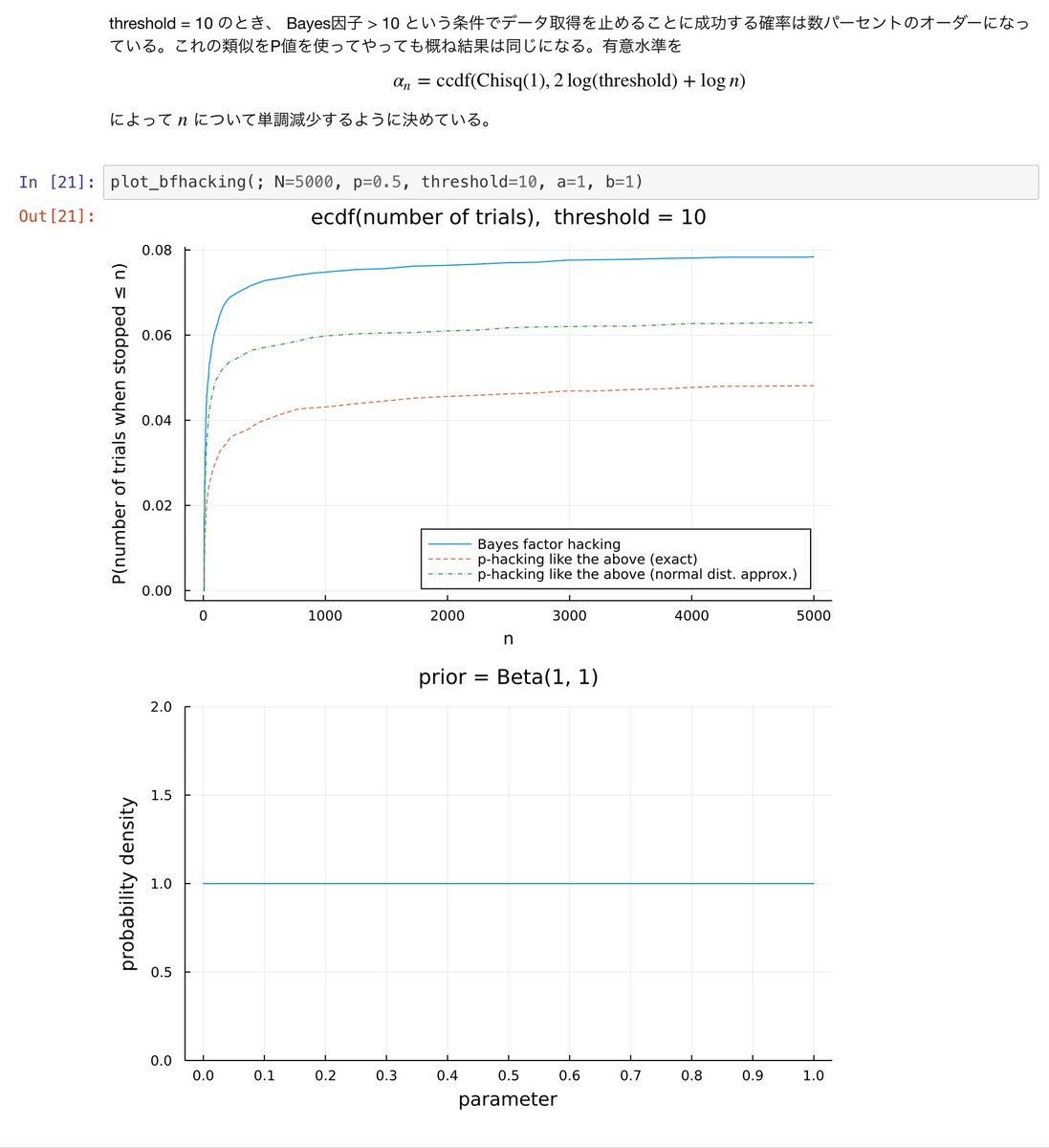
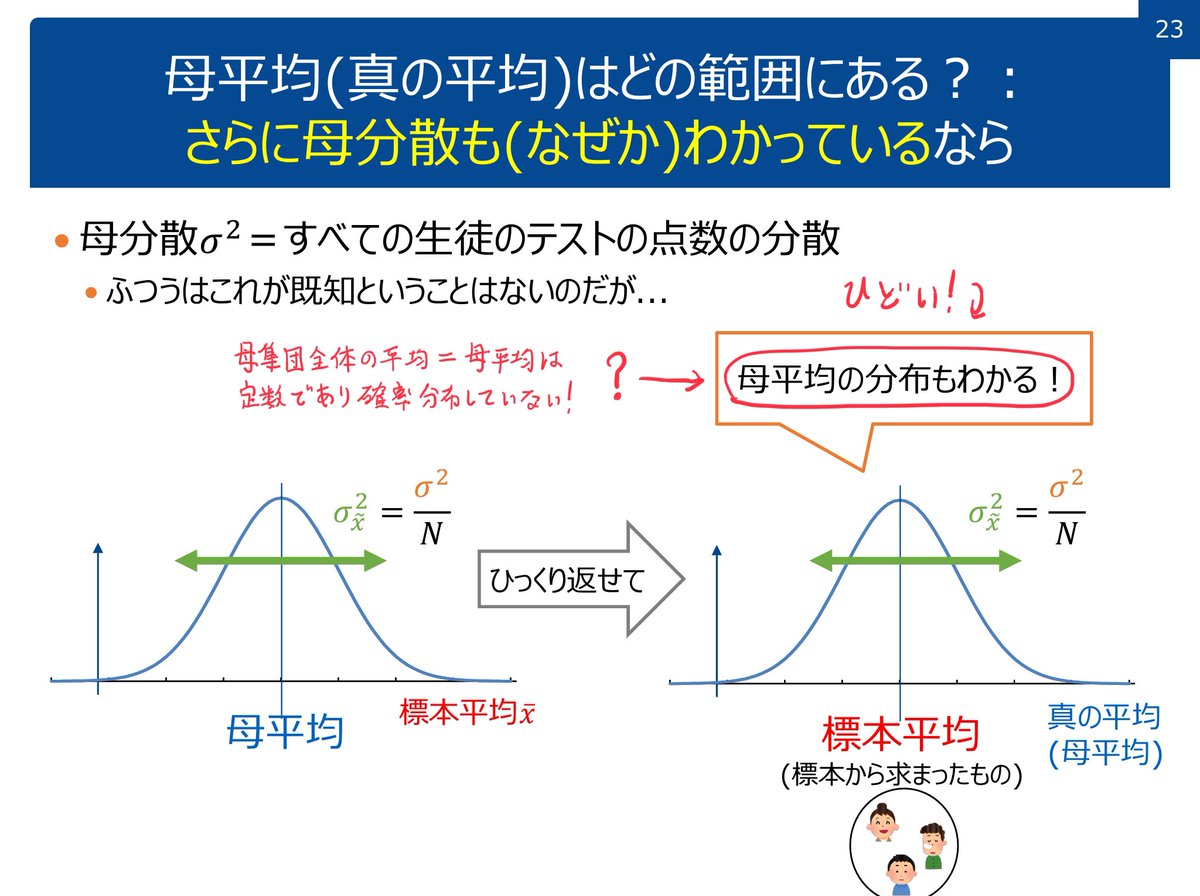
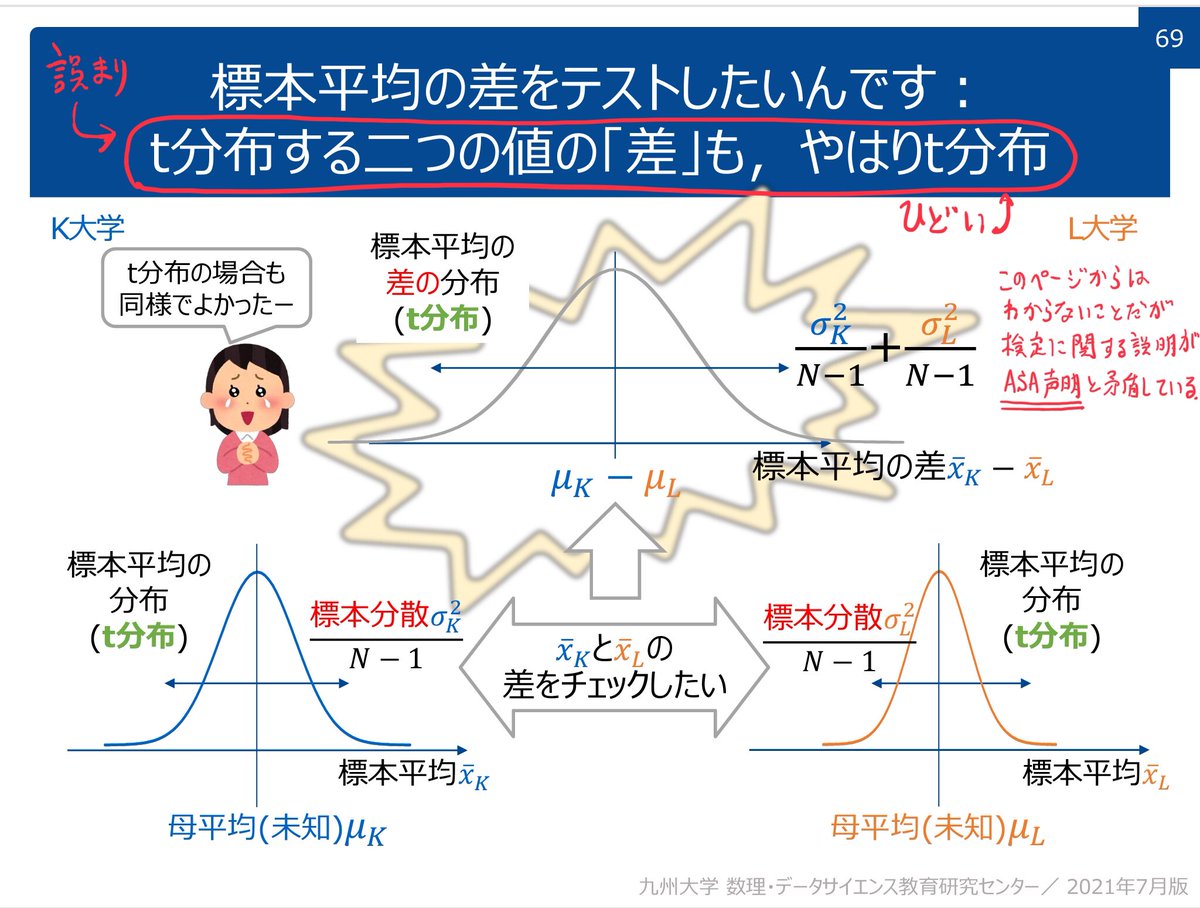
#統計 mdsc.kyushu-u.ac.jp/lectures の mdsc.kyushu-u.ac.jp/wp/wp-content/… の内容が滅茶苦茶。添付画像を参照。
①信頼区間の説明で「母平均の分布もわかる!」と書いてある。酷い!
②「t分布する二つに値の「差」も、やはりt分布」と書いてある。酷い!
③Wilcoxonの順位和検定は中央値の差の検定法ではない。


①信頼区間の説明で「母平均の分布もわかる!」と書いてある。酷い!
②「t分布する二つに値の「差」も、やはりt分布」と書いてある。酷い!
③Wilcoxonの順位和検定は中央値の差の検定法ではない。

#統計 P値や信頼区間に関するより現代的な知識は論文 journals.sagepub.com/doi/10.1177/02… で得られる。
統計的有意性とP値に関するASA声明 biometrics.gr.jp/news/all/ASA.p… は必読で、講義動画 ocwcentral.com/subjects/01GB4… には時代遅れな説明が書いてある教科書に批判的コメントがある。
これらの代替案に従えば無難。
統計的有意性とP値に関するASA声明 biometrics.gr.jp/news/all/ASA.p… は必読で、講義動画 ocwcentral.com/subjects/01GB4… には時代遅れな説明が書いてある教科書に批判的コメントがある。
これらの代替案に従えば無難。
#統計
mdsc.kyushu-u.ac.jp/lectures
↓
slideshare.net/ssuserf64eb4/s…
にも同様に酷い説明がある。
①真の平均が正規分布しているかのようなグラフの下に【真の平均は,95%の確率で,標本平均±1.96σ/√Nの範囲にある!】と書いてある!酷い。
②【t分布する二つの値の「差」も,やはりt分布】とある!酷い!



mdsc.kyushu-u.ac.jp/lectures
↓
slideshare.net/ssuserf64eb4/s…
にも同様に酷い説明がある。
①真の平均が正規分布しているかのようなグラフの下に【真の平均は,95%の確率で,標本平均±1.96σ/√Nの範囲にある!】と書いてある!酷い。
②【t分布する二つの値の「差」も,やはりt分布】とある!酷い!




#統計 「全部pだと困る問題」について。個人のノートでは
p₁(y|x,c)p₂(x|c)p₃(c)p₁(yₐ|a,c)
の代わりに、
p(y|x,c)p(x|c)p(c)p(y=yₐ|x=a,c)
と書くことにしている。引数名を固定して、引数xにaを代入する場合には引数をx=aと書くという方針。
#Julia言語 のp(; y, x, c)と同じ仕様を採用😊
p₁(y|x,c)p₂(x|c)p₃(c)p₁(yₐ|a,c)
の代わりに、
p(y|x,c)p(x|c)p(c)p(y=yₐ|x=a,c)
と書くことにしている。引数名を固定して、引数xにaを代入する場合には引数をx=aと書くという方針。
#Julia言語 のp(; y, x, c)と同じ仕様を採用😊
#Julia言語 での p(; x=y, μ=0, σ) のような書き方はこんな感じ。
using Distributions
p(; x, μ, σ) = pdf(Normal(μ, σ), x)
y = 1.96
σ = 1
p(; x=y, μ=0, σ)
using Distributions
p(; x, μ, σ) = pdf(Normal(μ, σ), x)
y = 1.96
σ = 1
p(; x=y, μ=0, σ)

プログラミング言語の仕様になっている書き方であれば、well-definedな表記法であることが保証されていると考えてよい。
#Julia言語 との類似は、変数名が違えば型も違うことにすると、同一の名前の函数(メソッド)の多重ディスパッチの仕組みによって、より完璧になる。
#Julia言語 との類似は、変数名が違えば型も違うことにすると、同一の名前の函数(メソッド)の多重ディスパッチの仕組みによって、より完璧になる。
#統計 2009年頃に、添付画像の場合に傾向スコア法を使うとバイアスが生じたりしないのか、という質問にルービン先生がまともに答えることができなかった件はもっと知られてよいと思う。
この件については、ルービン先生的な因果推論を学んだ人達もルービン先生個人に批判的になるべきだと思いました。
この件については、ルービン先生的な因果推論を学んだ人達もルービン先生個人に批判的になるべきだと思いました。

#統計 ある程度以上、統計的因果推論について学んだ人であれば、Cによる条件付けで調整すると、EのOutcomeへの効果にバイアスが生じ、因果効果の見積もりを誤る危険性があることを理解しているはずです。
易しい話です。
易しい話です。

#統計 ルービン先生は、「この場合の因果推論では、傾向スコア法に限らず、Cによる条件付けをしてはいけない」とクリアに答えればよかった。
ルービン先生は単にCによる条件付けに警告を発し、警告する機会を与えてくれたことについて、質問者にお礼を述べればよかった。
ルービン先生は単にCによる条件付けに警告を発し、警告する機会を与えてくれたことについて、質問者にお礼を述べればよかった。

#数楽 差分作用素をTf(n)=f(n+1)と書く。
a,b,cが異なるとき、
A aⁿ + B bⁿ + C cⁿ
は(T-a)(T-b)(T-c)の作用で消える。
(bⁿ-aⁿ)/(b-a)のb→aの極限naⁿ⁻¹なので
A aⁿ + A' naⁿ⁻¹ + C cⁿ
は(T-a)²(T-c)の作用で消える。続き
a,b,cが異なるとき、
A aⁿ + B bⁿ + C cⁿ
は(T-a)(T-b)(T-c)の作用で消える。
(bⁿ-aⁿ)/(b-a)のb→aの極限naⁿ⁻¹なので
A aⁿ + A' naⁿ⁻¹ + C cⁿ
は(T-a)²(T-c)の作用で消える。続き
#統計 c=a+hとおくと、
cⁿ = aⁿ + naⁿ⁻¹h + n(n-1)/2 aⁿ⁻² h² + O(h³)
なので、h→0のとき
(cⁿ - aⁿ - naⁿ⁻¹h)/h² →n(n-1)/2 aⁿ⁻².
ゆえに
A aⁿ + A' naⁿ⁻¹ + A'' n(n-1)/2 aⁿ⁻² = (nの2次以下の多項式) aⁿ
は(T-a)³の作用で消える。
一般の場合も同様。
cⁿ = aⁿ + naⁿ⁻¹h + n(n-1)/2 aⁿ⁻² h² + O(h³)
なので、h→0のとき
(cⁿ - aⁿ - naⁿ⁻¹h)/h² →n(n-1)/2 aⁿ⁻².
ゆえに
A aⁿ + A' naⁿ⁻¹ + A'' n(n-1)/2 aⁿ⁻² = (nの2次以下の多項式) aⁿ
は(T-a)³の作用で消える。
一般の場合も同様。
#数楽 特性方程式が重解を持つときにはJordan標準形を使うと覚えてしまった人がいるかもしれませんが、重解を持たない場合からの極限で重解を持つ場合も理解できます。
系を摂動したときの解の挙動の変化は重要なので、重解を持つ場合を持たない場合で近似することも重要です。
系を摂動したときの解の挙動の変化は重要なので、重解を持つ場合を持たない場合で近似することも重要です。
#統計 統計分析の背後には常にモデルがあり、統計的因果推論の場合には特に
* モデルを変えるべきときには変えなければいけない。
* 変更後のモデルに関する結果が変更前のモデルに関する結果から得られる場合がある。
が基本的。たぶん、パールさん達の方針は概念的にこのように要約される。続く
* モデルを変えるべきときには変えなければいけない。
* 変更後のモデルに関する結果が変更前のモデルに関する結果から得られる場合がある。
が基本的。たぶん、パールさん達の方針は概念的にこのように要約される。続く
#統計 例えば、変数XとYの関係を調べたいとき、Xが他の変数Zに影響されて決まる状況(例えば観察研究)と、ZのXへの影響を断ち切ってXのZと無関係に決まるようにした状況(例えばランダム化{比較,対照}試験)では、別の統計モデルを使う必要があります。
続く
続く
#統計 現象の背後にある法則は同一であっても、データの取得の仕方が異なれば、データの生成の仕方を記述する統計モデルも別のものにする必要がある。
こういうことはわざわざ言われなくても、当たり前だと言えないようでは、科学的な会話自体が不可能になるだろう。
続く
こういうことはわざわざ言われなくても、当たり前だと言えないようでは、科学的な会話自体が不可能になるだろう。
続く
#統計 以前にも述べたことですが、
ism.ac.jp/editsec/toukei…
情報量規準 AIC の統計科学に果たしてきた役割
小西 貞則
2019
の添付画像の部分はひどいです。
BICもあるKL情報量(+モデルによらない定数)の(大胆な)推定値になっていることを小西さんは理解していないっぽい。
リンクに続く
ism.ac.jp/editsec/toukei…
情報量規準 AIC の統計科学に果たしてきた役割
小西 貞則
2019
の添付画像の部分はひどいです。
BICもあるKL情報量(+モデルによらない定数)の(大胆な)推定値になっていることを小西さんは理解していないっぽい。
リンクに続く

#統計 続き
以前に述べていたことは以下のリンク先すれっどにある。
BICは対数周辺尤度の-2倍の大胆な近似とみなされ、対数周辺尤度の-1倍の標本の確率的揺らぎに関する期待値は
あるKL情報量+モデルによらないある定数
に一致している。
渡辺澄夫『ベイズ統計の理論と方法』を参照。
以前に述べていたことは以下のリンク先すれっどにある。
BICは対数周辺尤度の-2倍の大胆な近似とみなされ、対数周辺尤度の-1倍の標本の確率的揺らぎに関する期待値は
あるKL情報量+モデルによらないある定数
に一致している。
渡辺澄夫『ベイズ統計の理論と方法』を参照。
#統計 渡辺澄夫『ベイズ統計の理論と方法』のようなよく普及している教科書レベルの内容を理解していれば、【納得いきます】とは言ってはいけない案件。
その本に書いてあるように、BICの近似先の対数周辺尤度の-2倍は2KL情報量+定数の推定値だとみなされるので、情報量規準という呼び方は自然。
その本に書いてあるように、BICの近似先の対数周辺尤度の-2倍は2KL情報量+定数の推定値だとみなされるので、情報量規準という呼び方は自然。
#統計 「信頼区間」のような入門的な統計学用語を定期的にツイッターで検索しているのだが、
❌P値の使用はやめるべき
と
❌P値ではなく信頼区間を使うべき
がワンセットになっている誤解をよく見る。
⭕️95%信頼区間の各点には5%以上のP値達が乗っている
というイメージが見えていないらしい。
❌P値の使用はやめるべき
と
❌P値ではなく信頼区間を使うべき
がワンセットになっている誤解をよく見る。
⭕️95%信頼区間の各点には5%以上のP値達が乗っている
というイメージが見えていないらしい。
#統計 95%信頼区間は「P値が5%以上になるパラメータ値全体の集合」なので、本質的に
❌P値を使わずに、信頼区間を使うこと
は不可能です。
信頼区間に含まれるパラメータ値達の立場は同等ではなく、それぞれにP値というデータの数値とモデル+パラメータ値の相性の良さの指標が対応しています。
❌P値を使わずに、信頼区間を使うこと
は不可能です。
信頼区間に含まれるパラメータ値達の立場は同等ではなく、それぞれにP値というデータの数値とモデル+パラメータ値の相性の良さの指標が対応しています。
#統計 95%信頼区間の両端の点に対応しているP値は5%で、一般に100(1-α)%信頼区間の両端の点に対応してP値はαになります。
αを動かして、さまざまな幅の信頼区間を計算すれば、パラメータ値にどのようなP値が対応しているかがわかる、のように考えることができます。
αを動かして、さまざまな幅の信頼区間を計算すれば、パラメータ値にどのようなP値が対応しているかがわかる、のように考えることができます。
#統計 以下のリンク先で引用されている jakevdp.github.io/blog/2014/06/1… のExample 2: Jaynes' Truncated Exponential の内容がひどかったので、Jaynes(1976) bayes.wustl.edu/etj/articles/c… の関連箇所を見たらもっとひどかったので、ひどさが分かるようにノートを作りました。
↓
github.com/genkuroki/publ…
↓
github.com/genkuroki/publ…
#統計 Jaynes(1976) bayes.wustl.edu/etj/articles/c… (doi.org/10.1007/978-94…)のpp.196-198がびっくりするぐらい酷い。
__不適切な__信頼区間の構成法と平坦事前分布のベイズ信用区間を比較して、信頼区間を強くdisり、さらにp.198辺りでそのことについて講演したときの様子を偉そうに説明している。


__不適切な__信頼区間の構成法と平坦事前分布のベイズ信用区間を比較して、信頼区間を強くdisり、さらにp.198辺りでそのことについて講演したときの様子を偉そうに説明している。



#統計 統計学の内容以前に人間性が疑わしく思えて来そうなほど偉そうに書いている。
私には、単にJaynesさんは切断指数分布モデル(truncated exponential distribution model)の場合に、適切な信頼区間の構成法を見付けることができなかっただけに見えました。
↓
github.com/genkuroki/publ…
私には、単にJaynesさんは切断指数分布モデル(truncated exponential distribution model)の場合に、適切な信頼区間の構成法を見付けることができなかっただけに見えました。
↓
github.com/genkuroki/publ…
#統計 n回中k回奇数の目が出たというデータが得られたとき、
pᵏ(1-p)ⁿ⁻ᵏ
を最大化するpの値k/nを奇数の目が出る確率の推定値とするのが、二項分布モデルでの最尤法に一致します。
その最尤法では、n回中k回奇数の目が出たら、奇数の目が出る確率はk/nだと推定される。非常に安易!続く
pᵏ(1-p)ⁿ⁻ᵏ
を最大化するpの値k/nを奇数の目が出る確率の推定値とするのが、二項分布モデルでの最尤法に一致します。
その最尤法では、n回中k回奇数の目が出たら、奇数の目が出る確率はk/nだと推定される。非常に安易!続く
#統計 データからの最も安易な推定法は、シンプルなモデルを使った最尤法に一致することが多いです。
上の例では、3回中3回とも奇数の目が出ると、奇数の目が出る確率は3/3=1だと推定される。
この推定結果は真実を意味するわけでも何でもなくて、特定の方法による単なる推定結果に過ぎません。
上の例では、3回中3回とも奇数の目が出ると、奇数の目が出る確率は3/3=1だと推定される。
この推定結果は真実を意味するわけでも何でもなくて、特定の方法による単なる推定結果に過ぎません。
#統計 最尤法については、入門的な教科書の多くに妙な説明がよく書いてあります。
東大出版会の『統計学入門』は最尤法に限らず統計学における基本概念についてことごとくミスリーディングな説明をしているのに、標準的教科書の地位を占めてしまった。
これが高等教育の現実で結構厳しい。
東大出版会の『統計学入門』は最尤法に限らず統計学における基本概念についてことごとくミスリーディングな説明をしているのに、標準的教科書の地位を占めてしまった。
これが高等教育の現実で結構厳しい。
#統計
データと統計モデルが与えられたときに、モデルのパラメータ値にP値を対応させる函数をP値函数と呼びます。
P値函数全体の情報は尤度函数全体の情報に近似的に等しくなる場合が多い。
その場合には、P値函数が最大になるパラメータ値は最尤法による点推定の結果に近似的に等しくなる。続く
データと統計モデルが与えられたときに、モデルのパラメータ値にP値を対応させる函数をP値函数と呼びます。
P値函数全体の情報は尤度函数全体の情報に近似的に等しくなる場合が多い。
その場合には、P値函数が最大になるパラメータ値は最尤法による点推定の結果に近似的に等しくなる。続く
#統計 さらに、尤度函数全体の情報はベイズ統計での事後分布の情報にも近い。(事前分布の違いしかない(笑))
このように、Rothmanさん達の疫学の有名教科書がすすめているP値函数全体を使うという考え方は、尤度函数全体の様子を見ることとの関係を通して、ベイズ統計と地続きで繋がっています。
このように、Rothmanさん達の疫学の有名教科書がすすめているP値函数全体を使うという考え方は、尤度函数全体の様子を見ることとの関係を通して、ベイズ統計と地続きで繋がっています。
#統計 データと統計モデルから決まる
P値函数、尤度函数、事後分布の3つ
はほぼ同じような使い方をできる統計量になっています。
こういう理解の仕方ができれば、「主義が違う別の統計学がある」という有害な言説に騙されることなく、柔軟に統計学的ツールを使いこなし易くなると思われます。
P値函数、尤度函数、事後分布の3つ
はほぼ同じような使い方をできる統計量になっています。
こういう理解の仕方ができれば、「主義が違う別の統計学がある」という有害な言説に騙されることなく、柔軟に統計学的ツールを使いこなし易くなると思われます。
#統計 繰り返し述べていることですが、95%信頼区間の誤解する可能性の低い定義の仕方は「データから有意水準5%の検定で棄却されない(統計モデルの)パラメータの範囲」です。
例えば、パラメータは「ワクチンの効果」の指標を意味していたりする。
例えば、パラメータは「ワクチンの効果」の指標を意味していたりする。
#統計 「検定で棄却されないこと」は「データからはそういう可能性があることに配慮し続ける必要があるという程度のことしか言えない」ということに過ぎず、棄却されないから正しいかのように考えてはいけない。
これは検定論のイロハのイにあたること。
これは検定論のイロハのイにあたること。
#統計 例えば、ワクチンの効果の大きさと解釈されるパラメータを持つ統計モデルを適切に設定したとき、データから計算したそのパラメータの95%信頼区間が0をまたいでいたとする。
#統計 添付画像下段はよくあるベイズ版95%信用区間(確信区間)の最高事後密度(HPD)版です。95%の部分は0から1の間の任意の実数に一般化できる。
添付画像上段のベイズ版P値は「信頼区間と検定が表裏一体」という原理を適用して定義されています。
nbviewer.org/github/genkuro…
添付画像上段のベイズ版P値は「信頼区間と検定が表裏一体」という原理を適用して定義されています。
nbviewer.org/github/genkuro…
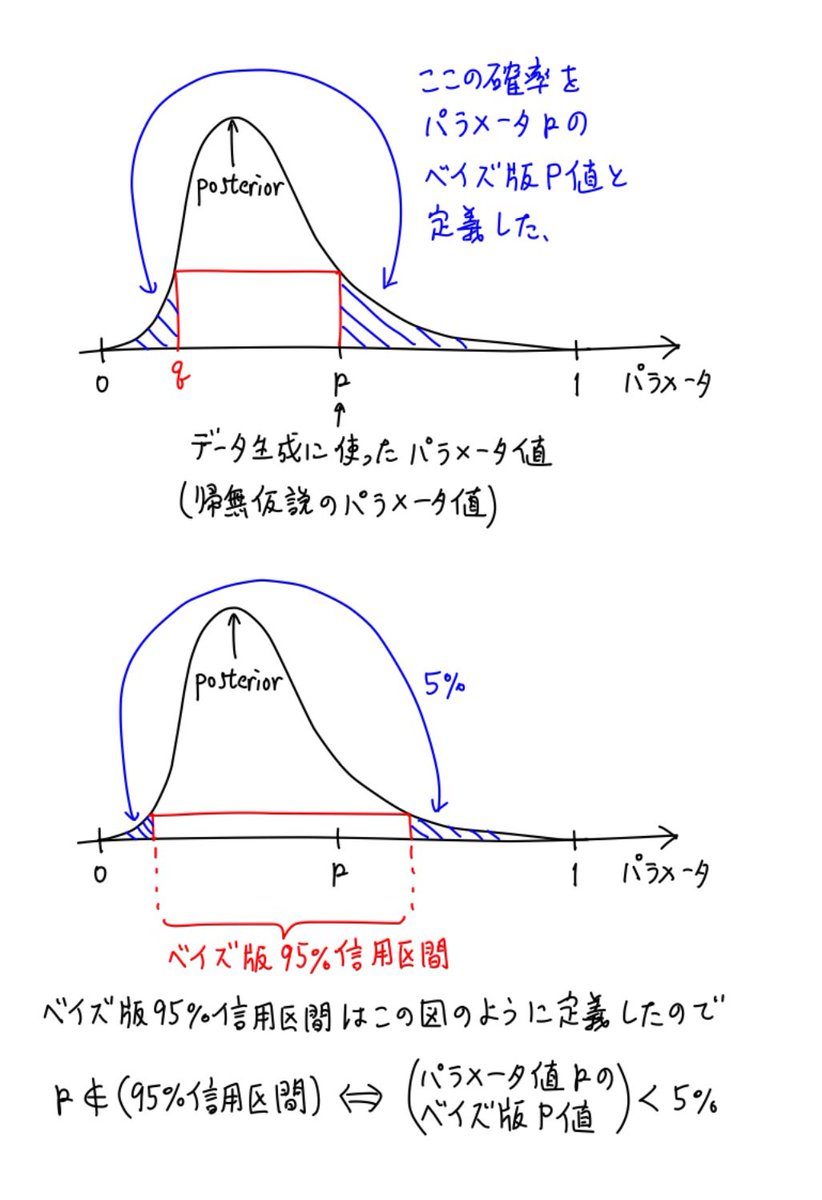
#統計 ベイズ版95%信用区間もベイズ版のP値も事後分布の情報だけを使って定義されており、通常の信頼区間やP値の作り方とは異なります。
しかし、数学には定義が全然違う量がある条件のもとでほぼ同じ値になることを証明できる場合が多数あって、解析学の基本的な考え方になっています。
しかし、数学には定義が全然違う量がある条件のもとでほぼ同じ値になることを証明できる場合が多数あって、解析学の基本的な考え方になっています。
#統計 実践的には無視できる違いしかない2つの数学的量を使った分析や推論は平等な扱いをする必要があります。
❌定義の違いは規範の違いから来ている。違いを無視できるほど同じ値になるとしても、それらは異なる使い方をされなければいけない。
などと言うと、単なるトンデモさんになってしまう。
❌定義の違いは規範の違いから来ている。違いを無視できるほど同じ値になるとしても、それらは異なる使い方をされなければいけない。
などと言うと、単なるトンデモさんになってしまう。
#統計 いやあ、これにはマジでびっくりした。😱
ベイズ版95%信用区間(確信区間)がゼロをまたがなくなるまでNを増やす行為は、P値が5%を切るまでNを増やすp-hacking行為と(小さな誤差を除けば)数学的に同等です。
P値が5%を切るまでNを増やすp-hacking行為の是非も規範の問題で済ませられる?
ベイズ版95%信用区間(確信区間)がゼロをまたがなくなるまでNを増やす行為は、P値が5%を切るまでNを増やすp-hacking行為と(小さな誤差を除けば)数学的に同等です。
P値が5%を切るまでNを増やすp-hacking行為の是非も規範の問題で済ませられる?
#統計 2020年3月に出版された豊田秀樹さんの本には、ベイズ統計では【データを取り増しても】よいし【事前登録~も必要ありません】と言っています。(他にも色々!)
これを「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と解釈する人達が出ることを危惧していました。
これを「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と解釈する人達が出ることを危惧していました。

#統計 より正確に言えば、同様の言説を他で見た人達が、「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と既に信じている場合もあるのではないかと思いました。
これ、めちゃくちゃまずくないですか?
これ、めちゃくちゃまずくないですか?
に訂正があるので注意!
「ある閾値以上大きくなる」の「ある閾値以上」が文字数のプレッシャに負けて抜け落ちてしまった。
具体的な計算例の方を見れば誤解は起こらないはず。
「ある閾値以上大きくなる」の「ある閾値以上」が文字数のプレッシャに負けて抜け落ちてしまった。
具体的な計算例の方を見れば誤解は起こらないはず。
続き
#統計 確率密度函数 p(x) = exp(-φ(x))/Z における ∫p(x)dx=1 にするための規格化定数 Z が不明の状況で、分布p(x)のサンプル(i.i.d.な乱数列)を数値的に得たい場合は多い。
函数φ(x)の情報だけから分布p(x)∝exp(-φ(x))の乱数列を作りたい。
MCMC法はそのための方法の1つ。
函数φ(x)の情報だけから分布p(x)∝exp(-φ(x))の乱数列を作りたい。
MCMC法はそのための方法の1つ。
#統計 MCMC法に分類される乱数列の生成法は色々ある。
HMC法ではφ(x)のgradientの情報が必要になる。
φ(x)が与えられれば、自動的にそのgradientも計算できるようにしてくれる自動微分は実際に使ってみると確かに非常に便利です。
HMC法ではφ(x)のgradientの情報が必要になる。
φ(x)が与えられれば、自動的にそのgradientも計算できるようにしてくれる自動微分は実際に使ってみると確かに非常に便利です。
#統計 「自動微分とは逆伝搬法のことだ」と誤解しているように見える発言を見たことがあるが、逆伝搬法は自動微分の手続きをある種の状況で高速化するための手法の1つに過ぎない。
行列A,B,C,DについてA(B(CD))と((AB)C)Dでは行列のサイズによって計算効率が大きく違う場合がある。更なる一般化あり。
行列A,B,C,DについてA(B(CD))と((AB)C)Dでは行列のサイズによって計算効率が大きく違う場合がある。更なる一般化あり。
#統計
⭕️正規分布に従う母集団から標本を無作為に取ってきてそのサイズと平均と不偏分散から95%信頼区間を求めた時に、その区間の中に95%の確率で母平均が含まれる。
は正しいです。ただし、確率的に揺らぐのは標本や信頼区間の側で、母平均は固定されています。続く
⭕️正規分布に従う母集団から標本を無作為に取ってきてそのサイズと平均と不偏分散から95%信頼区間を求めた時に、その区間の中に95%の確率で母平均が含まれる。
は正しいです。ただし、確率的に揺らぐのは標本や信頼区間の側で、母平均は固定されています。続く
#統計
❌正しくは、「母集団から標本を無作為に取ってきて、そのサイズと平均と不偏分散から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」という意味です。
は誤り。「正しくは」と訂正しようとしている所が単純に間違っています。訂正は無用。続く
❌正しくは、「母集団から標本を無作為に取ってきて、そのサイズと平均と不偏分散から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」という意味です。
は誤り。「正しくは」と訂正しようとしている所が単純に間違っています。訂正は無用。続く
#統計 「95%信頼区間の95%は確率ではなく、割合である」という信頼区間の定義に反する自明に間違っている主張をわざわざ広めて大恥をかいている人たちは一体どういうつもりなのか?
詳しくは私のツイログを参照
↓
twilog.org/genkuroki/sear…
詳しくは私のツイログを参照
↓
twilog.org/genkuroki/sear…
#統計 せっかく作ったので教育用のノートブックを放流
#Julia言語
nbviewer.org/github/genkuro…
二項分布のある種の極限でPoisson分布が得られる(添付画像③④)のと同じように、負の二項分布のある種の極限でガンマ分布が得られる(添付画像①②)。



#Julia言語
nbviewer.org/github/genkuro…
二項分布のある種の極限でPoisson分布が得られる(添付画像③④)のと同じように、負の二項分布のある種の極限でガンマ分布が得られる(添付画像①②)。




#統計 r=3, p=1/(5N)の負の二項分布を1/N倍でスケールして得られる分布のcdfはN=100でα=3, θ=5 のガンマ分布のcdfにほぼぴったり一致している。
離散分布と連続分布の比較は累積確率分布函数(cdf)のプロットで比較すると楽です。
#Julia言語
nbviewer.org/github/genkuro…
離散分布と連続分布の比較は累積確率分布函数(cdf)のプロットで比較すると楽です。
#Julia言語
nbviewer.org/github/genkuro…

#統計 この極限はそれぞれの分布の意味が分かっていれば「当然そうなる」と思える類のものです。
#統計 推定推測推論用に用意したパラメータθ付きの確率分布モデルp(x|θ)を前提とした
パラメータθの真の値は決まっている vs. パラメータθは確率分布している
という争いの枠組みは、私から見ると、
同類どうしの内ゲバ
に過ぎない。
推定推測推論用モデルの外側から来るリスクに無頓着。
パラメータθの真の値は決まっている vs. パラメータθは確率分布している
という争いの枠組みは、私から見ると、
同類どうしの内ゲバ
に過ぎない。
推定推測推論用モデルの外側から来るリスクに無頓着。
#統計 推定推測推論用に用意したパラメータθ付きの確率分布モデルp(x|θ)を前提とした上で、パラメータθの値は決まっているが未知なので、最悪の場合の損失を最小化するように意思決定する、というミニマックス法を使っていても、モデル自体が大外ししているリスクは考えていない。
#統計 推定推測推論用に用意したパラメータθ付きの確率分布モデルp(x|θ)において、パラメータθが確率分布していると考えて、パラメータの分布についての損失の期待値を最小化するように意思決定する、というベイズ的意思決定論を使っていても、モデル自体が大外ししているリスクは考えていない。
minimal working examples抜きには曖昧過ぎて微妙に危険な感じ。よい推定、よい予測、よい意思決定の中身が不明過ぎる。
特に「意思決定」という言葉が「推定」や「予測」など任意の行動を決める意味が広い用語になっているせいで、「本当はよい意思決定を目指すべきだ」と誤解する危険性がある。続く
特に「意思決定」という言葉が「推定」や「予測」など任意の行動を決める意味が広い用語になっているせいで、「本当はよい意思決定を目指すべきだ」と誤解する危険性がある。続く
教科書によく書いてある意思決定論では、パラメータ付きのモデル(推定推測推論用のモデル、以下単にモデルという)の内部で「最悪の場合の最善手」(ミニマックス)や「期待リスク最小化」(事前分布を主観確率と解釈すれば主観内で計算した期待リスク最小化)を考えます。
続く。リスクの定義を決める損失函数として「推定の悪さ」「予測の悪さ」の指標にすれば「モデル内でのよい推定」「モデル内でのよい予測」が得られ、仮に「金銭的な損失」の指標にできれば「モデル内での金銭的に最適な意思決定」が得られます。
そういう話は確かに結構面白いです。続く
そういう話は確かに結構面白いです。続く