Discover and read the best of Twitter Threads about #超算数
Most recents (24)
最近ちょっと話題の中学校の数学の教科書にある「ねじれの位置」という用語についてですが、数学の理解には不要な用語であるとしっかり教えて行く必要があると私は思っています。
例えば「ねじれの位置にある線分の組み合わせはどれか?」のような試験問題を出した人には反省してもらう必要がある。
例えば「ねじれの位置にある線分の組み合わせはどれか?」のような試験問題を出した人には反省してもらう必要がある。
この手のことは他にもたくさんあり、近年、中学校数学の試験問題の質を大幅に下げていると思います。
「理解に不要な用語をわざわざ覚えたか」を問う有害な問題が理解度を問う問題であるかのように出題されているという問題。
「理解に不要な用語をわざわざ覚えたか」を問う有害な問題が理解度を問う問題であるかのように出題されているという問題。
子供に強制的に覚えさせたい用語については、強制する側がその強制が必要である理由を説明する責任があります。
それをせずに、その用語が不要な理由を私に質問するのは質問を急ぎ過ぎ。
それをせずに、その用語が不要な理由を私に質問するのは質問を急ぎ過ぎ。
#超算数 積分定数さんの観察から、増加と合併の区別を子供に強制する方針は80年代に確立したことが示唆された。このスレッドでは、増加と合併の指導の劃期となったのが1977年指導要領に際して書かれた小学校指導書であったことを示し、執筆をリードした坂間利昭の責任を明らかにしてゆく。
#超算数 四則演算の文章題を分類する試みは、1910年代には始まっている。当時、増加に相当するものは見えないが、1920年には萌芽が(64)。
大阪府池田師範学校附属小学校編『小学校に於ける復習法』池田町 (大阪府) 、池田師範学校附属小学校、1920年。dl.ndl.go.jp/info:ndljp/pid…
大阪府池田師範学校附属小学校編『小学校に於ける復習法』池田町 (大阪府) 、池田師範学校附属小学校、1920年。dl.ndl.go.jp/info:ndljp/pid…

#超算数 【総和を求むるもの】と【つぎ足すもの】が現代でいう合併と増加に相当することは、64頁に指示された国定教科書の対応箇所を参照すれば分かる。
文部省『尋常小學算術書』第3學年兒童用 東京 國定教科書共同販賣所、1919年。nierlib.nier.go.jp/lib/database/K…
[これ、国定第何期か分かる人います?]

文部省『尋常小學算術書』第3學年兒童用 東京 國定教科書共同販賣所、1919年。nierlib.nier.go.jp/lib/database/K…
[これ、国定第何期か分かる人います?]


#超算数 ことごとく正しいことを述べていても、証拠となる資料を引用していなければ、「観戦者」への説得力はゼロに近付き、証拠の資料抜きに信じてしまうような人達だけにアピールしてしまうことにもなります。
自分の主張の大部分に証拠資料を添付するようにした方がベターだと思いました。
自分の主張の大部分に証拠資料を添付するようにした方がベターだと思いました。
#超算数 算数教育界が100年以上ずっとおかしな教え方を続けているという問題については、具体的にどういう問題であるかが世間的にほとんど何も知られていません。
自分の意見を述べるよりも、事実を示す資料の拡散の方が重要であり、資料拡散のツイートをする人が増えないと非常にまずいと思います。
自分の意見を述べるよりも、事実を示す資料の拡散の方が重要であり、資料拡散のツイートをする人が増えないと非常にまずいと思います。
#超算数 最近、再拡散した方が良いと思って実際にそうした資料
#超算数 以前、よく知っている子供が「中3」ではなく、「小3」になって割り算を習ったことに気付いたので、速さ、距離、時間の計算が易しい問題を出したら、普通に正解しました。
生活の中で距離と時間について知っていて、「1時間で3km歩く」のような言い回しを理解できれば、公式は無用。続く
生活の中で距離と時間について知っていて、「1時間で3km歩く」のような言い回しを理解できれば、公式は無用。続く
#超算数 小3の子は、公式について一切習ってなくても、速さ、距離、時間の問題を普通に解ける、という話は以下のリンク先で引用した本にも書いてあります。
#超算数 小3の時点で「1時間に4kmずつ歩く」とか「1時間に50kmずつ車で進む」のような言い方をすれば、子供は理解できます。
それどころか、「2時間で100kmずつ進む」のように「単位量当たり」ではなく「2時間当たり」も理解できる。
「単位量当たりの~をみんな理解できない」は錯覚だと思います。
それどころか、「2時間で100kmずつ進む」のように「単位量当たり」ではなく「2時間当たり」も理解できる。
「単位量当たりの~をみんな理解できない」は錯覚だと思います。
#超算数 谷村省吾さんは遠山啓さんの言葉を孫引きしていますが、実際には遠山さんは彼自身による「量の理論」に基き、かけ算順序固定強制指導を正当化する酷い発言も残しています。
添付画像②を参照。
「量の理論」がその後の算数教育に与えた悪影響について谷村さんは知っているでしょうか?続く

添付画像②を参照。
「量の理論」がその後の算数教育に与えた悪影響について谷村さんは知っているでしょうか?続く
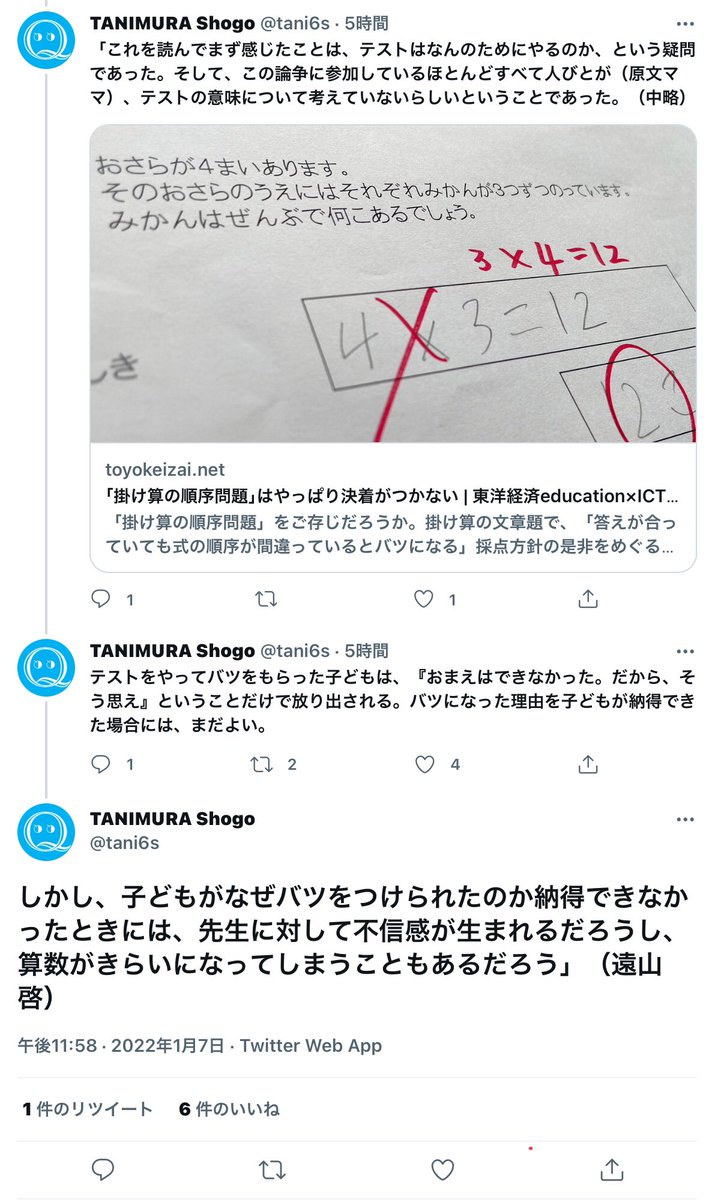

#超算数 遠山啓氏は、自身が広めた「内包量」という困りものの算数数学教育用語を用いてこう言った。
【乗法の交換法則が連続量にはまだ適用しないほうがよいとしたら〜外延量×内包量とは書かないほうがよいだろう】
【単価×分量~とは書くが~分量×単価〜とは書かない】
books.google.co.jp/books?id=Zaiaq…
【乗法の交換法則が連続量にはまだ適用しないほうがよいとしたら〜外延量×内包量とは書かないほうがよいだろう】
【単価×分量~とは書くが~分量×単価〜とは書かない】
books.google.co.jp/books?id=Zaiaq…

#超算数 「量の理論」についても教わってしまったのはまずかったと思います。
昔から数学関係者の一部には、遠山啓さんやその「量の理論」に好意的なせいで、遠山啓さん及びその弟子筋(特に銀林浩氏)が算数数学教育に与えた悪影響を無視する傾向があるという問題があります。
これは頭の痛い問題。
昔から数学関係者の一部には、遠山啓さんやその「量の理論」に好意的なせいで、遠山啓さん及びその弟子筋(特に銀林浩氏)が算数数学教育に与えた悪影響を無視する傾向があるという問題があります。
これは頭の痛い問題。

#超算数 見事に何が問題とされているかを全然理解できていない。
#超算数 【等号「=」の意味の違い】だと説明しようとしている点があまりにも杜撰すぎる。これはひどくデタラメな説明だと言って問題ない。
あと、常識的にはx=x+1やx=xも「その等式を満たす実数xの全体を求めよ」の形で方程式扱いされるので、添付画像の方程式の説明もおかしいです。
あと、常識的にはx=x+1やx=xも「その等式を満たす実数xの全体を求めよ」の形で方程式扱いされるので、添付画像の方程式の説明もおかしいです。

#超算数 【等号「=」の意味の違い】とする説明が批判されているのに、それとは違う杜撰な要約をして、以下のリンク先のように、等号「=」の意味の違いとは全然違う話を始めた。
しかも、その内容もかなり杜撰。
しかも、その内容もかなり杜撰。
子供のときに「くもわ図」や「きはじ図」「みはじ図」「はじき図」「木の下のハゲじじい図」(笑)で問題を解くことを教える先生に当たった人は、大人になった自分自身がそれで不自由を感じていなくても、「運が悪かった。そのような教え方は子供を害する」と思っておく必要があります。
❌「くもわ図」や「きはじ図」には算数が苦手な子を救う効果があるので、算数が苦手な子には「くもわ図」や「きはじ図」を教え込もう
と考えるのは非常にまずいです。
子供を害する(子供の頭を悪くする)教え方を、特に算数が苦手な子にはする習慣になると、その子が救われることがなくなる。😭
と考えるのは非常にまずいです。
子供を害する(子供の頭を悪くする)教え方を、特に算数が苦手な子にはする習慣になると、その子が救われることがなくなる。😭
算数が苦手な真の原因は「公式を暗記できないこと」ではなく、「算数だと常識に沿って考えることができなくなる」や「計算が苦手」な場合が多いと思います。
計算が苦手でも常識に沿って考えることができてかつ公式の使用を強制されなければ問題を解ける場合が増えます。続く
計算が苦手でも常識に沿って考えることができてかつ公式の使用を強制されなければ問題を解ける場合が増えます。続く
#超算数 かけ算順序問題について教育関係者の多くは「順序が逆なだけでバツにするのは好ましくない」と言います。
しかし、本音では「4人に3本ずつ鉛筆を配る場面で4×3と式を書く子はかけ算の意味を理解していない」と思っており、児童にかけ算の順序を教え込まなければいけないと思っていたりする。
しかし、本音では「4人に3本ずつ鉛筆を配る場面で4×3と式を書く子はかけ算の意味を理解していない」と思っており、児童にかけ算の順序を教え込まなければいけないと思っていたりする。
#超算数 質問の内容は可能な限り具体的なものにする必要があります。
例えば、添付画像1のように聞いてみるとよいかもしれません。
「②の式を2×5にする子も問題なくかけ算を理解しているとどの先生も思っている」言ってもらえたらやっと信用できます。
続く
例えば、添付画像1のように聞いてみるとよいかもしれません。
「②の式を2×5にする子も問題なくかけ算を理解しているとどの先生も思っている」言ってもらえたらやっと信用できます。
続く

#超算数
教科書出版社側は②で5×2としなければいけないことを教え込むためにこの問題を載せています。添付画像1の教科書のマニュアル本の記述を見て下さい。
そしてそういう問題を出す直前のページで交換法則が一般的に成立している理由を教える構成になっています(添付画像2)。

教科書出版社側は②で5×2としなければいけないことを教え込むためにこの問題を載せています。添付画像1の教科書のマニュアル本の記述を見て下さい。
そしてそういう問題を出す直前のページで交換法則が一般的に成立している理由を教える構成になっています(添付画像2)。


#超算数 式を書くだけで説明したことにしてしまう現代の算数教育における最悪の慣習が1924年までは遡れたということか!
悪名高いかけ算順序指導の歴史は100年を超えていることが分かっている。
平田華蔵『学習心理学講話: 教科本位』東京、南光社、1924年
dl.ndl.go.jp/info:ndljp/pid…
悪名高いかけ算順序指導の歴史は100年を超えていることが分かっている。
平田華蔵『学習心理学講話: 教科本位』東京、南光社、1924年
dl.ndl.go.jp/info:ndljp/pid…

#超算数
❌解答欄が「式 答え 」の形式になっていてかつ「式」を書くスペースが狭い
という現代の算数教育の典型的なスタイルに気付いて、小学生の面倒を見ている人達は恐怖を感じた方がよい。好ましいルールは
⭕️問題を解くために役に立つかもしれないことについて何を書いてもよい。
❌解答欄が「式 答え 」の形式になっていてかつ「式」を書くスペースが狭い
という現代の算数教育の典型的なスタイルに気付いて、小学生の面倒を見ている人達は恐怖を感じた方がよい。好ましいルールは
⭕️問題を解くために役に立つかもしれないことについて何を書いてもよい。
#超算数 理解がまだ途中の子にとっては、実際には問題を解くために役に立たないかもしれないが、その子自身が「もしかしたら」と期待していることについて何を書いてもよいことにしないとまずい。
「もとにする数」?しかも小3で。
これはひどいな。
こんな問題については一生理解する必要はありません。
この手の算数プリントに気付くたびに、うちではお母さんが素早く子に「こんなの理解しなくていい!」とはっきり言う方針になっています。
これはひどいな。
こんな問題については一生理解する必要はありません。
この手の算数プリントに気付くたびに、うちではお母さんが素早く子に「こんなの理解しなくていい!」とはっきり言う方針になっています。
算数教育界は「どんな数をもとにするか」のような算数教育界でしか通用しない子供が習得し難い用語を算数教育界の都合で使用する傾向があります。
そういう非常識で子供に優しくない人たちに、子供の側が合わせてやる必要はないです。
「自分ちではマル❤️」でいいと思いました。
そういう非常識で子供に優しくない人たちに、子供の側が合わせてやる必要はないです。
「自分ちではマル❤️」でいいと思いました。
#超算数 リンク先のような反応は頓珍漢。
実際、【どんな数をもとにすると】の意味がわからない、という大人側からの反応が続出している。
高等教育を受けた日本語話者であっても、その言い回しを理解できない。
国語的には【どんな数をもとにすると】という言い回しには教える価値がない。
実際、【どんな数をもとにすると】の意味がわからない、という大人側からの反応が続出している。
高等教育を受けた日本語話者であっても、その言い回しを理解できない。
国語的には【どんな数をもとにすると】という言い回しには教える価値がない。
#超算数 高校の教科書でも説明が結構雑い。
「式」という用語はひどく曖昧で、
* 1/x と (x + 1 - x)/x と (x-1)/(x(x-1)) は「式」として等しいのか?
という問いにこの教科書の読者は答えることができないと思う。
検定329 数研 新編数学II p.17
「式」という用語はひどく曖昧で、
* 1/x と (x + 1 - x)/x と (x-1)/(x(x-1)) は「式」として等しいのか?
という問いにこの教科書の読者は答えることができないと思う。
検定329 数研 新編数学II p.17

#超算数 最近の例の話題との関連では
* 1/x と (x + 1 - x)/x と (x-1)/(x(x-1)) は「式」として等しいのか?
だけではなく、
* 等しい「式」を函数とみなすときの定義域はいつも同じになるのか?
とも問いたい。
教科書の説明がひどく曖昧な問題は我々が指摘して来たことの1つ。
* 1/x と (x + 1 - x)/x と (x-1)/(x(x-1)) は「式」として等しいのか?
だけではなく、
* 等しい「式」を函数とみなすときの定義域はいつも同じになるのか?
とも問いたい。
教科書の説明がひどく曖昧な問題は我々が指摘して来たことの1つ。
#超算数 数学的本質を捉えた高校生の答案には難癖をつけるが、中高の数学の教科書の説明が不明瞭な点について何も問題にしない。
さすがにそれはまずいと思います。
(下手をすれば教科書に書いてあることと違うことをやっているから減点すると言い出しかねないのではないか?)
さすがにそれはまずいと思います。
(下手をすれば教科書に書いてあることと違うことをやっているから減点すると言い出しかねないのではないか?)
#数楽
多項式f∈ℝ[x]に「a∈ℝをf(a)∈ℝを対応させる函数」を対応させる写像は単射なので、多項式fとそれに対応する実数の函数を区別しなくも大丈夫。(無限体でもOK)
有限体F上の多項式g∈F[x]に「a∈Fをg(a)∈Fを対応させる函数」を対応させる写像は単射でないので、それらを同一視できない。
多項式f∈ℝ[x]に「a∈ℝをf(a)∈ℝを対応させる函数」を対応させる写像は単射なので、多項式fとそれに対応する実数の函数を区別しなくも大丈夫。(無限体でもOK)
有限体F上の多項式g∈F[x]に「a∈Fをg(a)∈Fを対応させる函数」を対応させる写像は単射でないので、それらを同一視できない。
#数楽 例えば二元体𝔽₂={0,1} (1+1=0)について、𝔽₂上の多項式としてxとx²は異なるが、𝔽₂上の函数としてはどちらも恒等写像になって等しくなってしまう。
xとx²を𝔽₂の2次拡大𝔽₄=𝔽₂[α] (α²=α+1)上の函数とみなしたものは互いに異なる。
こういう具体例がノータイムで出て来ることが大事。
xとx²を𝔽₂の2次拡大𝔽₄=𝔽₂[α] (α²=α+1)上の函数とみなしたものは互いに異なる。
こういう具体例がノータイムで出て来ることが大事。
#数楽 面倒なのは有理函数(多項式環の分数体の要素)に対応する「函数」の場合。
有理函数ごとに定義域も変わるので、異なる定義域を持つ函数達を同時に扱うための「処理」が必要になる。(これには複数の処方箋がある。)
結果的に、無限体の場合には、有理函数と対応する「函数」は同一視可能になる。
有理函数ごとに定義域も変わるので、異なる定義域を持つ函数達を同時に扱うための「処理」が必要になる。(これには複数の処方箋がある。)
結果的に、無限体の場合には、有理函数と対応する「函数」は同一視可能になる。
#超算数 【「1セットあたりの量」と「○セット」という概念の定着を目的にあえて縛りを設けていると考えれば納得.】とか言うお馬鹿さん達が継続して出て来ることが昔からよく知られています。
かけ算順序固定強制指導が実際に有害であることの間接的な証拠とみなせると思う。続く
かけ算順序固定強制指導が実際に有害であることの間接的な証拠とみなせると思う。続く
#超算数 現実の子供に関しては、同じ数を含む集まりが何セットあるかの状況把握と掛け算順序マスターであることは、現場の教師の調査で関係ないことが分かっています。
そして、その教師は、関係ないことを認めた上で、掛け算順序強制指導を強化しなければいけないと主張しています。
これが現実。
そして、その教師は、関係ないことを認めた上で、掛け算順序強制指導を強化しなければいけないと主張しています。
これが現実。
#超算数 掛け算順序が逆なら誤りとみなしたり、掛け算順序が逆なら理解していないとみなす行為は、算数教育の世界では100年以上の伝統を持っています。
これだけの伝統があると、掛け算順序指導が社会的に否定されると困る人達が沢山いることもよく分かる。
しかし、被害者は次世代を担う子供達。
これだけの伝統があると、掛け算順序指導が社会的に否定されると困る人達が沢山いることもよく分かる。
しかし、被害者は次世代を担う子供達。
Soraさんの意見にはいつも賛成です。
ただし、「立式」という用語は一般的な用語ではなく、算数教育では「場面や考え方を忠実に式に翻訳すること」という意味で使われており、たし算やかけ算の悪しき順序指導の根拠としても使われる言葉です。意味を代わりに簡単に説明させて下さい。 #超算数
ただし、「立式」という用語は一般的な用語ではなく、算数教育では「場面や考え方を忠実に式に翻訳すること」という意味で使われており、たし算やかけ算の悪しき順序指導の根拠としても使われる言葉です。意味を代わりに簡単に説明させて下さい。 #超算数
#超算数 順序固定強制指導を氷山の一角とする算数教育界の事情を何も知らないと、「立式」という普通の国語辞典に載っていない特殊な用語の意味を、「問題文をよんで、問題を解くために役に立ちそうな式を書くこと」のような無害な意味で解釈しがち。
実際にはもっと極端な意味で使われています。
実際にはもっと極端な意味で使われています。
#超算数 例:「4人に3本ずつ鉛筆を配るとき、全部で何本の鉛筆が配られますか?」に「式 4×3=12 答え 12本」と答えることを、「答えは正しいが立式は間違っている」とするのが、かけ算順序固定強制指導の典型例です。
4×3が誤りになるという意味を「立式」という特殊な用語は含んでいます!😱
4×3が誤りになるという意味を「立式」という特殊な用語は含んでいます!😱
数学市民さんという人がひどいことを言いまくっていた。
どういう人なのか知らないし、私のTLには登場しないし、検索しても発言が見当たらないと思ったら、なぜかミュートしていたようです。
色々謎が解決。
ビジネス数学にまつわる継続論争 - Togetter togetter.com/li/1679140 @togetter_jpより
どういう人なのか知らないし、私のTLには登場しないし、検索しても発言が見当たらないと思ったら、なぜかミュートしていたようです。
色々謎が解決。
ビジネス数学にまつわる継続論争 - Togetter togetter.com/li/1679140 @togetter_jpより
私のTL以外の空間で、そのひどい発言がまともだと思った人達が出て来たりしていて、それを気にする発言が出ていたんですね。
私のところにはその気にする発言しか流れて来ず、一体何が起こっているのだろうかと思っていました。
ツイッターでの話題にリアルタイムでついて行くのは私には難しい。
私のところにはその気にする発言しか流れて来ず、一体何が起こっているのだろうかと思っていました。
ツイッターでの話題にリアルタイムでついて行くのは私には難しい。
ミュートはそのままにしておくことにした。😊
#超算数
「(算数は)定義とか論理じゃないので」のようなことを、100年以上の伝統を持つ非常識な算数教育の伝統に沿って言う人達は基本的に嘘つき。
例えば、小2算数教科書での長方形と正方形の定義は非常に正確で小2の子にも「正方形は長方形の特別な場合であること」が分かるようになっています。
「(算数は)定義とか論理じゃないので」のようなことを、100年以上の伝統を持つ非常識な算数教育の伝統に沿って言う人達は基本的に嘘つき。
例えば、小2算数教科書での長方形と正方形の定義は非常に正確で小2の子にも「正方形は長方形の特別な場合であること」が分かるようになっています。

#超算数 長方形と正方形については、すでに小2算数教科書に正確な定義が噛み砕かれた形式で載っているのに、ちょー算数の伝統に則って算数の教え方を指南する人達が、小学校の先生達をおかしな方向に誘導している。
ちょー算数信者の発言は大体において全部「嘘」だと思っておく方がよいです。
ちょー算数信者の発言は大体において全部「嘘」だと思っておく方がよいです。
#超算数 小2の子であっても、正方形を見せて、すべての角が直角かどうかを聞いてみて、全部直角だと答えた直後に、教科書にある長方形の定義を読ませて、その条件を満たしていることを確認させると、正方形も長方形の一種であることをすぐに理解できます。
教科書に書いてあるルールに従うだけ。
教科書に書いてあるルールに従うだけ。

#超算数
【超算数をインストールされた人、なぜか再生産を行う傾向にある】
そうなる理由↓
日本で算数教育で飯を食って行きたい場合には、ちょー算数マスターになると、就職先が増えたり、出世できる可能性が増えたりする。
ちょー算数には100年以上の伝統に支えられた社会的基盤があります。
【超算数をインストールされた人、なぜか再生産を行う傾向にある】
そうなる理由↓
日本で算数教育で飯を食って行きたい場合には、ちょー算数マスターになると、就職先が増えたり、出世できる可能性が増えたりする。
ちょー算数には100年以上の伝統に支えられた社会的基盤があります。
かけ算順序問題が新聞で話題にされても、ダメージも受けない理由は、社会的に硬い基盤を持っているから。
子供の保護者側は自分ちの子が被害を受けずに通過すれば発言を続ける意欲は減ります。
ちょー算数マスターになると算数教育界で出世してより良い地位に転職できるかもしれない。
この対比。
子供の保護者側は自分ちの子が被害を受けずに通過すれば発言を続ける意欲は減ります。
ちょー算数マスターになると算数教育界で出世してより良い地位に転職できるかもしれない。
この対比。
例えば、算数の教科書の著作者リストに載っている人達がちょー算数についてどのような考え方を持っているか、どこでその考えを身につけたのか、どのような経歴で算数の教科書の著作者まで出世できたのか、などについては調べる価値があります。
これ面倒な作業で結構大変。
これ面倒な作業で結構大変。
まさに数学教育の闇
kanielabo.org/edmath/thirdme…
RIMS研究集会
教育数学の一側面-高等教育における数学の多様性と普遍性-
研究代表者:岡本和夫
副代表者:蟹江幸博
RIMS420号室,2018.2.13-2018.2.16
↓
大島 利雄(城西大学)
大学における数学教育の問題点と工夫
kanielabo.org/edmath/thirdme…
kanielabo.org/edmath/thirdme…
RIMS研究集会
教育数学の一側面-高等教育における数学の多様性と普遍性-
研究代表者:岡本和夫
副代表者:蟹江幸博
RIMS420号室,2018.2.13-2018.2.16
↓
大島 利雄(城西大学)
大学における数学教育の問題点と工夫
kanielabo.org/edmath/thirdme…

全然、関係ない話題と繋げてしまうことになるが、上で引用した大島さんの文章は【妖怪について扱った文章であるにも関わらず具体的な妖怪の実例がほとんど皆無で抽象論に終始している】の類のものとは正反対。
ものすごく具体的!
ものすごく具体的!
私は大島さん的な文章が好きで、意味のある具体例がない抽象的な文章は有害だと考えている。
数学の研究者間では、抽象化・一般化はやろうと思えば幾らでもできるので、価値ある抽象化・一般化であることを示す具体的な例を示さないとダメだという非常に良い習慣があると思う。例がショボいとアウト。
数学の研究者間では、抽象化・一般化はやろうと思えば幾らでもできるので、価値ある抽象化・一般化であることを示す具体的な例を示さないとダメだという非常に良い習慣があると思う。例がショボいとアウト。
他にも似たような反応がありますが、小5の算数の教科書にある割合の3つの公式を覚えさせたり、「もとにする量」「比べられる量」という割合の概念を理解するために不要な用語を使うことを児童に強制していたら、教わっている子の将来が暗くなると思います。
教科書通りの教え方がまずい証拠がある。
教科書通りの教え方がまずい証拠がある。
お勧めしたいのは以下の2冊の本です。
実際に子供に算数を教えていたら楽しんで読めると思います。
amazon.co.jp/dp/4101370311
お母さんは勉強を教えないで
見尾 三保子
このタイトルはひどいし、内容とも一致していません。
内容の大部分は算数や数学の真っ当な教え方の話です。
2冊目紹介に続く
実際に子供に算数を教えていたら楽しんで読めると思います。
amazon.co.jp/dp/4101370311
お母さんは勉強を教えないで
見尾 三保子
このタイトルはひどいし、内容とも一致していません。
内容の大部分は算数や数学の真っ当な教え方の話です。
2冊目紹介に続く
2冊目
amazon.co.jp/dp/4788508435
学力低下をどう克服するか―子どもの目線から考える
2003/3/25
吉田 甫
タイトルを見ても分からないことですが、教科書通りの教え方の対照群と実験的な教え方を、実際に授業をしてみて比較してみた研究結果が書いてあります。分数と割合の教え方を詳しく扱っています。
amazon.co.jp/dp/4788508435
学力低下をどう克服するか―子どもの目線から考える
2003/3/25
吉田 甫
タイトルを見ても分からないことですが、教科書通りの教え方の対照群と実験的な教え方を、実際に授業をしてみて比較してみた研究結果が書いてあります。分数と割合の教え方を詳しく扱っています。
#超算数 我々一般人が捨てなければいけない思い込みは、日本の算数教育界で影響力を持ち、社会的にも立派な人扱いされている人たちが、算数について穏健で常識的なことを言っているだろうという思い込み。
算数の教科書を見れば分かる。
0は偶数だが、0を2の倍数扱いすると誤りだとする方針!
算数の教科書を見れば分かる。
0は偶数だが、0を2の倍数扱いすると誤りだとする方針!

#超算数 おそらく最も驚くべき倍数に関する教材がこれ。
amazon.co.jp/dp/4491026491
小学校算数 板書で見る全単元・全時間の授業のすべて 5年〈上〉
2011/3/1
山本 良和 (監修), 筑波大学附属小学校算数部 (編集)
より
0が倍数から除かれている様子を見よ!

amazon.co.jp/dp/4491026491
小学校算数 板書で見る全単元・全時間の授業のすべて 5年〈上〉
2011/3/1
山本 良和 (監修), 筑波大学附属小学校算数部 (編集)
より
0が倍数から除かれている様子を見よ!


#超算数 算数の教科書ではことごとく「0は倍数に入れない」ということになっていることについては以下のリンク先を参照。
【私自身も直方体の面積[ママ]は縦×横×高さでないとダメだと言う学年主任と組んだこともあります。来年以降そういった先生に当たっても困らないよう丸にしつつも順序を気にする先生もいるから気をつけろと伝えています。】
学年主任の側に「ごめんなさい」と言わせるべき。子の側に言うことじゃない。
学年主任の側に「ごめんなさい」と言わせるべき。子の側に言うことじゃない。

#超算数
(悪しき)掛算順序指導の定番の1つは「3×2ならウサギの耳が3本になっちゃう」の類です。
この教え方の狙いは子供に「あれ?」と思わせること。3がウサギの耳の本数じゃないことを子供が分かっていることを前提にしている。
数の意味ではなく、掛算順序を教える方法になっています。
(悪しき)掛算順序指導の定番の1つは「3×2ならウサギの耳が3本になっちゃう」の類です。
この教え方の狙いは子供に「あれ?」と思わせること。3がウサギの耳の本数じゃないことを子供が分かっていることを前提にしている。
数の意味ではなく、掛算順序を教える方法になっています。
#超算数 で、とある先生による調査によれば、子供が書く掛算順序と掛算使用のための絵を正しく描けることの間に関係はない。
ところが、その先生はそういう結果が得られたのに、掛算の意味=掛算の順序をもっとしっかり教え込まなければいけないと結論を出しています。
mnavidata.edu-c.pref.miyagi.jp/manage/wp-cont…
ところが、その先生はそういう結果が得られたのに、掛算の意味=掛算の順序をもっとしっかり教え込まなければいけないと結論を出しています。
mnavidata.edu-c.pref.miyagi.jp/manage/wp-cont…

#超算数
チョー算数問題のある一部分は劣った思考法に陥ったまま大人になった人達が、自分自身が劣っていることを自覚できずに、次世代の子供達を自分と同レベルの劣った存在にするような教え方に賛成しているという問題。
自覚がないので、自分自身が劣っていることを隠すことさえできない。
チョー算数問題のある一部分は劣った思考法に陥ったまま大人になった人達が、自分自身が劣っていることを自覚できずに、次世代の子供達を自分と同レベルの劣った存在にするような教え方に賛成しているという問題。
自覚がないので、自分自身が劣っていることを隠すことさえできない。
#超算数 しかし、それは問題の一部分に過ぎず、本丸は、算数に関するデタラメな考え方をしている側が、算数教育の世界における人の出世の流れをコントロールできる社会的な仕組みだと思う。
その辺にいる雑魚をどんなに蹴散らせても、チョー算数マスター達が算数教育の世界で正々堂々と出世して行く。
その辺にいる雑魚をどんなに蹴散らせても、チョー算数マスター達が算数教育の世界で正々堂々と出世して行く。
#超算数 算数の教科書執筆者の中にいるチョー算数マスター達が困るような正当な情報をどのように流すかが多分重要だと思う。
我々が抱えている問題はそのための知識がまだ足りないということ。
チョー算数マスターが算数の教科書の執筆者まで出世できる仕組みを我々は十分に理解していない。
我々が抱えている問題はそのための知識がまだ足りないということ。
チョー算数マスターが算数の教科書の執筆者まで出世できる仕組みを我々は十分に理解していない。
#統計 新刊の大塚淳著『統計学を哲学する』を近所の本屋で買って来ました。まだp.91にしか目を通していないのですが、
【データに基づく信念の改定というベイズ流の考え方】
とか
【ベイズ統計~ベイズ主義では確率は主観的な信念の度合いを測るもの】
と書いてあった!これはひどいと思いました。
【データに基づく信念の改定というベイズ流の考え方】
とか
【ベイズ統計~ベイズ主義では確率は主観的な信念の度合いを測るもの】
と書いてあった!これはひどいと思いました。

#統計 現実の統計分析や機械学習でベイズ統計の技術が「データに基づく信念の改定」としては普通使われていません。
数学的モデルとしての確率分布は使われていますが、モデル内における確率をわざわざ「主観的な信念の度合い」などと解釈したりしません。続く
数学的モデルとしての確率分布は使われていますが、モデル内における確率をわざわざ「主観的な信念の度合い」などと解釈したりしません。続く
#統計 去年の12月に出版された浜田宏他著『社会科学のための ベイズ統計モデリング』という本を見れば、社会科学の分野においても理解度の高い人たちにとって、ベイズ統計はすでに「主観確率」の「ベイズ主義」によるものではなくなっていることが分かります。続く
【#超算数 みたいな俺ルールを押し付ける公立学校の教師をみると、やっぱり私立の小中高を目指す優先度は高いね。】
注意・警告!優秀な算数の先生が欲しいという理由で「算数教育専門家」とみなされる教師を雇っている小学校は、チョー算数のメッカのような教え方になっていると推測されます。続く
注意・警告!優秀な算数の先生が欲しいという理由で「算数教育専門家」とみなされる教師を雇っている小学校は、チョー算数のメッカのような教え方になっていると推測されます。続く
#超算数 実際に、「がんばって私立の小学校に入学できたのに、掛け算順序指導を含むおかしな教え方をされた」という保護者の嘆きを見たことがあります。続く
#超算数 チョー算数指導は算数教育について熱心に勉強した先生ほど行う可能性が高い。
そうなってしまう理由は、算数教育の世界のカーストで上位になるためにはチョー算数マスターになることが必要だからです。
チョー算数で子供を苦しめる行為は、歴史ある伝統と社会制度によって支えられています。
そうなってしまう理由は、算数教育の世界のカーストで上位になるためにはチョー算数マスターになることが必要だからです。
チョー算数で子供を苦しめる行為は、歴史ある伝統と社会制度によって支えられています。
