Discover and read the best of Twitter Threads about #VisualAlgebra
Most recents (7)
Now that my #VisualAlgebra class is in the books, I want to post a long "meta thread" of all 16 weekly threads, with daily summaries. Here's my entire class, including lectures, HW, & exams, in one convenient place.
And stayed tuned for some surprise announcements below!👇🧵
And stayed tuned for some surprise announcements below!👇🧵
We started #Week1 of #VisualAlgebra with a few quotes from "A Mathematician's Apology" on the beauty of mathematics, and then saw Cayley diagrams for the symmetries of the rectangle and triangle.
In #Week2 of #VisualAlgebra, we explored the Rubik's cube, more Cayley diagrams, group presentations, the impossibility of the word & halting problems, and we classified all frieze groups.
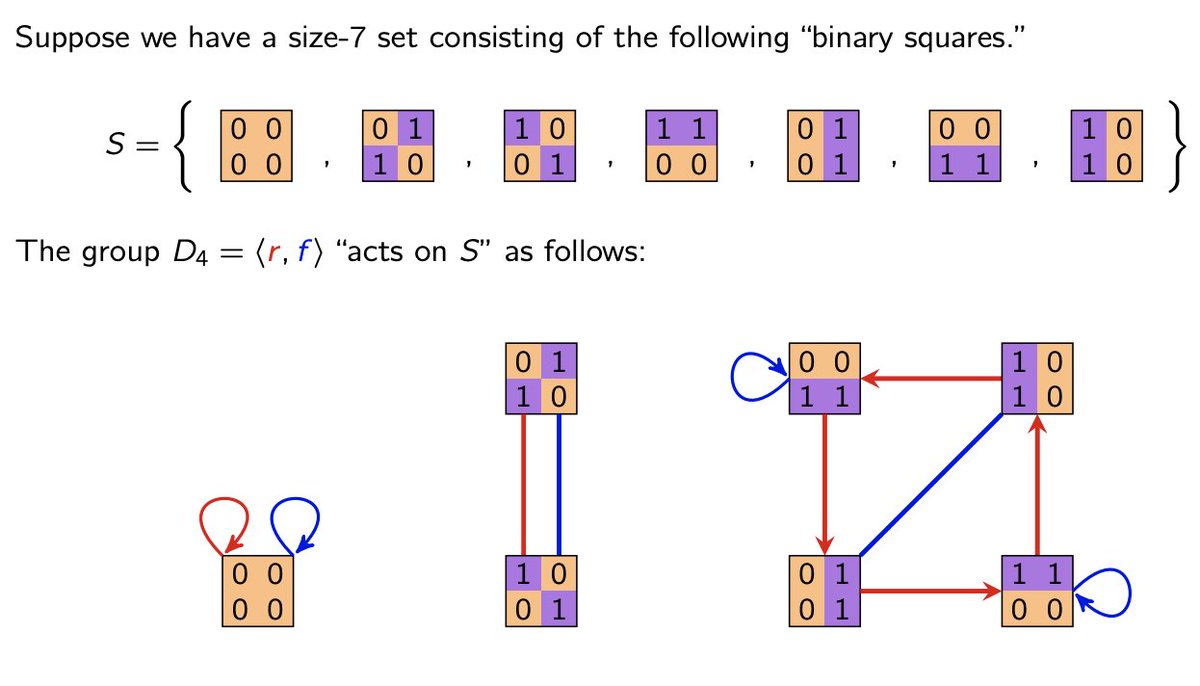
I woke up a few days ago with the sobering realization: actually, I do NOT really understand groups actions.
Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. 😳
Let me explain, I think some of you might enjoy this!
1/12 🧵👇
Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. 😳
Let me explain, I think some of you might enjoy this!
1/12 🧵👇
See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).
Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?
2/12
Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?
2/12
For example, how many of the following are possible?
Before reading on, see if you can answer this, and generalize to arbitrary groups.
There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.
3/12
Before reading on, see if you can answer this, and generalize to arbitrary groups.
There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.
3/12
Finishing up our🧵👇 #VisualAlgebra class in #Week15 with divisibility and factorization. I'm a little short on visuals, but here are two really nice ones on what we'll be covering, made by @linguanumerate.
Henceforth, we'll assume that R is an integral domain.
1/8 Mon
Henceforth, we'll assume that R is an integral domain.
1/8 Mon
The integers have nice properties that we usually take for granted:
--multiplication commutes
--there aren't zero divisors
--every nonzero number can be factored into primes
--any 2 nonzero numbers have a unique gcd and lcm
--the Euclidean algorithm can compute these
2/8 M
--multiplication commutes
--there aren't zero divisors
--every nonzero number can be factored into primes
--any 2 nonzero numbers have a unique gcd and lcm
--the Euclidean algorithm can compute these
2/8 M
Some, but not all of these hold in general integral domains. This is what we'd like understand!
If b=ac, we say "a divides b", or "b is a multiple of a".
If a | b and b | a, they're "associates", written a~b.
HW: a~b iff they differ by a unit (i.e., a=bu).
3/8 M
If b=ac, we say "a divides b", or "b is a multiple of a".
If a | b and b | a, they're "associates", written a~b.
HW: a~b iff they differ by a unit (i.e., a=bu).
3/8 M
We started #Week11 of #VisualAlgebra with a new diagram of one of the isomorphism theorems. I made this over spring break. The concept is due to Douglas Hofstadter (author of "Gödel, Escher, Bach"), who calls this a "pizza diagram".
1/14 Mon 🧵👇
1/14 Mon 🧵👇
Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed.
Recall the analogy for Aâ‹ŠB:
A = automorphism, B = "balloon".
2/14 M
Recall the analogy for Aâ‹ŠB:
A = automorphism, B = "balloon".
2/14 M
Next, we asked when a group G is isomorphic to a direct product or semidirect product of its subgroups, N & H.
Here are two examples of groups that we are very familiar with.
3/14 M
Here are two examples of groups that we are very familiar with.
3/14 M
We started #Week7 in #VisualAlgebra yesterday with the tower law.
Here are two ways to think about it. One involves cosets as "boxes" in a grid, and the other is in terms of the subgroup lattice: to find the index [H:K], just take the product of the edges b/w them.
1/8 Mon
Here are two ways to think about it. One involves cosets as "boxes" in a grid, and the other is in terms of the subgroup lattice: to find the index [H:K], just take the product of the edges b/w them.
1/8 Mon
Pause for a quick comment about cosets in additive groups. Don't forget to write a+H, rather than aH. Here's a nice way to see the equality of a left coset and a right coset.
2/8 M
2/8 M
Next, we proved that if [G:H]=2, then H is normal. Here's a "picture proof": one left (resp., right) coset is H, and the other is G-H.
3/8 M
3/8 M
WEEK 2 of #VisualAlgebra! This is only Lecture #2 of the class.
Monday was MLK Day, but on Wed, we learned about the Rubik's cube! I got to show up my rare signed cube with Ernő Rubik himself from 2010! Did a shout out to @cubes_art's amazing talents.
1/8 W
Monday was MLK Day, but on Wed, we learned about the Rubik's cube! I got to show up my rare signed cube with Ernő Rubik himself from 2010! Did a shout out to @cubes_art's amazing talents.
1/8 W
We learned some neat facts about the Rubik's cube, like how the group has just 6 generators, but 4.3 x 10^{19} elements, and a Cayley diagram with diameter of 20 or 26, depending on whether you count a 180 degree twists as 1 or 2 moves.
2/8 W
2/8 W
I showed 3 different groups of order 8, and asked if any are isomorphic. At this point, all they know about what that means is that two groups must have identical Cayley diagrams *for some generating set*.
3/8 W
3/8 W
WEEK 1: first lecture of #VisualAlgebra.
"The mathematician's patterns, like the painter's or the poet's must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way."
― G.H. Hardy, A Mathematician's Apology
1/4
"The mathematician's patterns, like the painter's or the poet's must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way."
― G.H. Hardy, A Mathematician's Apology
1/4
We have not yet defined a group. Rather, we are exploring the intuition of them via symmetries. This will *motivate the axioms*, rather than the other way around.
What properties does this group have what might not hold more generally?
2/4
What properties does this group have what might not hold more generally?
2/4
For further insight, consider the symmetries of a triangle. This motivates the idea of relations, and why this "group calculator" tool is useful.
I got so many really good questions and comments in class today. How often does that happen on *Day 1* of abstract algebra??
3/4
I got so many really good questions and comments in class today. How often does that happen on *Day 1* of abstract algebra??
3/4
